長い間、仕事ではパイプライン系ツールを書くことが多くなり、幾何学や物理などの数学とはだいぶ疎遠になってしまいました。
最近になって、やっとHoudiniを業務で使用させてもらえる環境が与えられたこともあり、これも良い機会ということで、これからしばらくの間、数学の勉強や復習とリハビリを兼ね、Processingの名著 [NATURE OF CODE] の内容を、Houdiniを使って追いかけていきたいと思います。
はじめに
I.1 ランダムウォーク
オブジェクトが累積的にランダムな方向に動く動作。
I.2 ランダム・ウォーカークラス
・ランダム・ウォーカークラスを定義
Houdiniでカスタムノードを定義することはクラスを定義することと言えそう。
ただし、現時点では継承等の仕組みがあるか不明なので、あくまでもクラスもどきの定義と解釈しています。
ここでは、まずSubnetをクラスとしてとらえつつ、その内部に、ランダムウォークする点群を複数含むオブジェクトを定義する。
・擬似ランダム値
一般的に、コンピュータ上で乱数を生成するランダム関数は実際には周期性があるので擬似的なランダム関数と言える。
ただし、周期が非常に長いため、実質的に真の乱数計算関数と言って差し支えない。
I.3 確率と一様分布(離散)
HoudiniでVEX関数のrandom()を使った場合、特定の値が出現する確率はほぼ一定。
具体例として、4種類の値を生成するランダム関数があるなら、それぞれの値が出現する確率はほぼ均等で約25%になる。
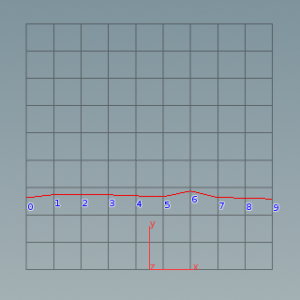
random()から出力される0~1のfloat値を0~9のint値にマッピング。
乱数を1200回発生させ、マッピング後の整数値に対応するIDを持つポイントをその都度+Y方向に移動した結果、多少のばらつきはあるものの、ほぼ均等な値が生成されていることがわかる。
このように、起こりうる結果がほぼ均等に現れる確率の分布を、一様分布と呼ぶ。
他の例としては下記のようなものもある。
- コイントスの確率
1/2 = 0.5 = 50% - 全トランプ52枚からA4枚のいずれかを引く確率
4/52 = 0.077 = 約8% - 全トランプ52枚からダイヤのカード13枚のいずれかを引く確率
13/52 = 0.25 = 25% - 1つのサイコロを振り、1の目が出る確率。
1/6 = 0.166 = 約17%
・確率と非一様分布
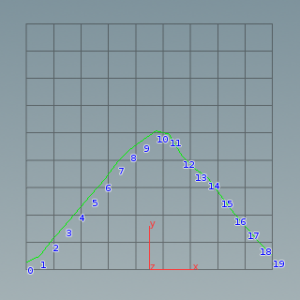
一様分布の項で作成したランダム関数を2つ足しあわせ、値が出現する回数を計測してみる。
結果、グラフは中央値が高く、山なりになるのがわかる。
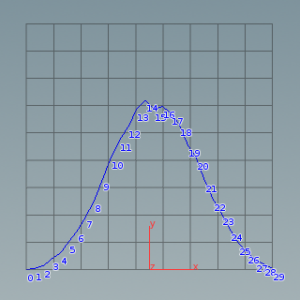
今度は、3つのランダム関数を使って同様の計算をしてみる。
より顕著に、山なりになる。
サイコロを3個振る場合を考えてみると理由は簡単。
合計値が最小の3または最大の18になるのは1または6のゾロ目の時のみで非常に確率が低いのに対し、合計値が中央付近の10になるケースはより多くの組み合わせが考えられる。
・乱数に偏りを持たせる
乱数を元に、予め用意された動作を選択する際、結果に偏りを持たせるには。
- 乱数を元に得たい結果がリストにまとめられているケース
結果がリスト内に登場する回数を操作して確率に偏りを持たせる<<擬似コード>> results = [1,2,3,4,5] → [1,1,1,2,3,3,4,5,5,5]
- 乱数の値の範囲に応じて結果が決定するケース
結果に対応する乱数の範囲を操作して偏りを持たせる<<擬似コード>> if random < 0.1: return 10 elif random < 0.2: return 20 else: return 30
I.4 ランダム値の正規分布(ガウス分布)
ランダムな要素が平均値付近に集中する確率分布を正規分布やガウス分布(Gaussian)、ラプラス分布(Laplacian)などと呼ぶ。
[参考サイト] NtRand – 正規分布
http://www.ntrand.com/jp/normal-distribution-single/
例として、無作為に選んだ人々の身長の分布を考える。
百歩譲っていくら確率が0ではないと言っても、身長0.1cmの人や身長10mの人はそうそういない。
平均慎重と言われている165cm付近が最も多くなるはず。
・ベル型曲線
確率の平均[μ]と標準偏差[σ]により求められる、確率分布を表すグラフ。
- 平均:μ
起こりうる値の平均値。 - 標準偏差:σ
偏差とは、値と平均値の差。
平均偏差は全偏差の平均。
標準偏差は、分散の平均の平方根。(※分散は偏差の2乗)
・乱数の生成(random)
HoudiniにおけるVEX関数のrandom()は、0~1の範囲で一様分布の乱数を発生させる事ができる。(その他にも、3Dノイズなども出力できる)
・乱数の生成(noise)
HoudiniにおけるVEX関数のnoise()はシンプルなパーリンノイズ。
正規分布をもとに乱数を発生させる。
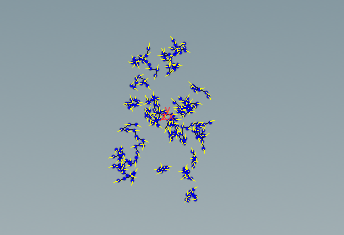
ループ中で新たなポイントを作成しながら乱数を発生させ、@P.xに与えていくと、各ポイントは下図のように配置されていく。

図では色が薄く見づらいが、μ=0.5、σ=1の正規分布で乱数が生成され、x=0.5の付近でより高密度にポイントが作成されていることがわかる。
※1マス=0.25
I.5 ランダム値のカスタム分布
- 分岐条件を乱数をもとに判定(レヴィフライト風アルゴリズム)
乱数の発生を一様分布でも正規分布でもない独自のものにしたい場合のテクニック。正規分布の乱数中で、時折「突発的」にレンジの大きな乱数を発生させたい場合は、現在の乱数生成の機会が「突発的」なものであるか判定し、突発的であると判断された場合、結果の範囲が大きな乱数を発生させるようにする。## 擬似コード incident = random(1) if incident < 0.1: randValue = random(-100,100) else: randValue = random(-1,1)上の例では、incidentが0.1以下(10%)の確率でレンジの大きな乱数を生成している。
- 出力が条件に適合するまで乱数の生成を試行する(モンテカルロ法風アルゴリズム)
値が大きければ大きいほど選ばれやすくしたい場合のテクニック。
乱数を2つ使い、片方がもう片方より大きかった場合に乱数を出力する。def montecarlo(): while 1: r1 = random(0,1) r2 = random(0,1) if r1 <= r2: return r2
I.6 パーリンノイズ(よりスムーズな手法)
有機的なものの表現には、ランダム値の中にも連続性が必要になる。
その場合、ランダムかつ連続的に変化する値を出力するnoise関数を使用するとよい。
HoudiniのVEX関数 noise()は、正規分布に近い連続的でランダムな値を返すパーリンノイズ関数で、整数を与えるとすべて同じ値(0.5)を返すようになっているので、引数は極力整数値にしないように注意する。
## noise()の使用例 f@dx = fit(noise(@Time+(@ptnum*0.339)+offset),0,1,-1,1);
・疑問
Mayaの場合、noise()関数は周期性を感じさせない上に、出力される値も-1~1の範囲にきっちり収まるようになっている。
そのため、単純なフレーム番号を引数にするだけで延々と連続的なランダム値を生成し続け、その値を係数にして角度の変化などを計算する際、変化のレンジにただ掛け合わせるだけでよかった。
Houdiniのnoise()関数は、整数値を与えると全く同じ値が返る上に、結果が正規分布で得られるため、Mayaのnoise()関数と全く同じ感覚では使えない。
正規分布のおかげで結果を有機的にしやすい反面、変化幅の上下限をきっちり決めづらくとても気持ち悪く感じてしまう。(例えば毎フレーム何らかのオブジェクトの角度を変化させたい時、0~180度の角度範囲を上下限とし、-1~1の範囲の係数をかけて使いたい場合など)
もしかしてMayaのnoise()に近い関数があるんだろうか?(誰かご存知でしたら教えて下さい)
・パーリンノイズによるランダムウォーク

・2次元のノイズ
パーリンノイズは1~4次元の値を引数に取り、同様に1~4次元の値を出力できる。
・@P.yにもnoise(x,y)の結果を適用

※わかりやすくするため、頂点数とカラーのレンジを調整済み
I.7 展望
この章では、自然現象をシミュレートする際に必要となる確率や乱数を学習した。
ランダム性を取り入れることで、より自然で複雑な要素を作成できる。
だがしかし、同じアルゴリズムにばかり頼ってしまうと結果的にパターンが透けて見えてしまい、結果が退屈な仕上がりになる場合もあるので、より多くの手法を身につけ、引き出しを増やし、様々なニーズに臨機応変に対応できるスキルを磨くことが大事。
[資料]
NtRand – 確率分布Navi
http://www.ntrand.com/jp/gallary-of-distributions/
何か間違いなどあればツッコミいただけると喜びます。
よろしくお願いします。